C++ · 25430 watchers
modern-cpp-tutorial
📚 Modern C++ Tutorial: C++11/14/17/20 On the Fly | https://changkun.de/modern-cpp/
oulongqi's repos on GitHub
Go · 321 watchers
occamy
🖥️ a modern remote desktop proxy written in Go
Go · 226 watchers
midgard
⛰️ Universal clipboard sharing service (supports macOS/Linux/Windows/iOS)
177 watchers
german-tutorial
德语零基础教程
Shell · 151 watchers
dotfiles
personal development settings
Go · 38 watchers
pkg
🥼 personal Go codebase
TypeScript · 34 watchers
gp
🏭 Geometry Processing at LMU Munich
JavaScript · 29 watchers
changkun-blog-clients
Changkun's Blog Desktop&Mobile Client
Python · 26 watchers
gitcheat
Cheating Git Contribute History
Go · 26 watchers
gopherchina2023gogpu
Talk "Go on GPU" in GopherChina 2023
Go · 25 watchers
generics
Deprecated! See https://github.com/golang-design/go2generics.
Go · 24 watchers
Go-Questions
从问题切入，串连 Go 语言相关的所有知识，融会贯通。
Go · 19 watchers
cgo-benchmarks
Benchmarks between Cgo, Go and C
TypeScript · 18 watchers
cg1
📺 Computer Graphics at LMU Munich
17 watchers
LeapDocCN
LeapMotion 官方文档中文翻译
TeX · 16 watchers
lmu-thesis-latex
📔 A LaTeX template for LMU Master/Bachelor theses (paper+slides).
Go · 12 watchers
chat
ChatGPT in command line
Go · 9 watchers
bo
🔍 Bayesian Optimization in Go
C++ · 9 watchers
compiler-of-training
西南民族大学2015年春季学期秦沿海《编译原理》课程设计的Training语言的词法、语法、语义分析源代码。
Go · 9 watchers
office
🏢 Is Changkun in the Office?
Go · 8 watchers
blog
✍️ Changkun's Blog
Python · 8 watchers
muenchen-termin
Automated appointment booking service for muenchen.de
6 watchers
computer-networks
Lecture notes of Computer Networks and Distributed Systems
6 watchers
eng-practices
Google 工程实践文档 (中文版)
5 watchers
claude-design-docs
Claude Code Design Docs
Go · 5 watchers
enhance
A Go package for enhancing photographs (adjusting brightness, contrast, etc.)
HTML · 5 watchers
login
Lightweight SSO Login System
4 watchers
awesome-go-graphics
awesome graphics projects in Go
PostScript · 4 watchers
BachelorThesis
Designing Alternative Contact-free Control Modalities for Smart Watches
Go · 3 watchers
apreserve
apple store shopping appointment checker
Jupyter Notebook · 3 watchers
gitchain
GitHub repositories meets cryptocurrencies.
3 watchers
gold-miner
🥇掘金翻译计划，可能是世界最大最好的英译中技术社区，最懂读者和译者的翻译平台：
Go · 3 watchers
gomat
Matrix package with cache-aware lock-free tiling optimization in Go
Go · 3 watchers
infloop
The Human in the Infinite Loop
3 watchers
intelligence-in-the-loop
Open Source Artifacts for Ph.D. Dissertation: The Intelligence in the Loop
Go · 3 watchers
main
🏠 The entrance of changkun.de
2 watchers
applied-ml
Applied Machine Learning Paper Reading List.
2 watchers
changkun
Github Homepage Profile
Go · 2 watchers
goid
retrieve a goroutine id in Go 1
C++ · 2 watchers
ImageProc
西南民族大学2015年春季学期雷开彬《数字图像处理（上）》实验课源代码。
2 watchers
knowledge
Changkun's Knowledge
Go · 2 watchers
pgo-glimpse
A Glimpse to Profile-guided Optimization in Go
C++ · 1 watchers
AugmentedTouch
Discovering how we use sensor data with touch behaviour to adapt user interface on mobile devices.
Go · 1 watchers
cat
a replacement to the UNIX's cat written in Go
Go · 1 watchers
clickhouse-prototype
Go · 1 watchers
cyclemod2
enable import cycle using modules? (part 2)
Go · 1 watchers
fyne
Cross platform GUI in Go based on Material Design
Python · 1 watchers
github-follower-net
Analytical Tool for Personal Github Follower Network Centrality
Go · 1 watchers
go
The Go programming language
Python · 1 watchers
goalless-agents
Intrinsic preferences of AI coding agents under underspecified prompts: 7 experiments across 15 models (Claude, Gemini, GPT), 405 sessions.
C · 1 watchers
guacamole-server
Mirror of Apache Guacamole Server
Stylus · 1 watchers
hexo-theme-next
Personal Awesome Changes for Hexo Next Theme
Go · 1 watchers
libtorch-go
libtorch Go wrapper for model inference
Python · 1 watchers
life-simulator
A terminal-based life simulator built entirely with Python's standard library. Cellular automata, fluid dynamics, particle systems, quantum circuits, neural networks, ecology, game theory, fractals, and more — all rendered with curses at 60 fps. No external dependencies.
HTML · 1 watchers
machine-translation-detection
A machine translation detection service.
TeX · 0 watchers
acmart
(Optimized) ACM Publication Template
0 watchers
acmart-official
ACM consolidated LaTeX styles
Go · 0 watchers
adventOfCode2021
TeX · 0 watchers
agentic-morphogenesis
Research "Architectural Morphogenesis in Autonomous Agent Systems"
Python · 0 watchers
agents-byzantine-tolerance
Experiment on Byzantine fault tolerance for agents
Python · 0 watchers
arxiv
changkun's arXiv preserver
0 watchers
arxiv-latex-cleaner
arXiv LaTeX Cleaner: Easily clean the LaTeX code of your paper to submit to arXiv
PHP · 0 watchers
assignments-16-17
Public repo for student-contributed solutions for the assignments (Online Multimedia @ LMU)
TeX · 0 watchers
bibtex-tidy
Cleaner and Formatter for BibTeX files
Python · 0 watchers
blockchain
Build blockchain from scratch
C · 0 watchers
cellular-automaton-explorer
A fully interactive, zero-dependency cellular automaton explorer for the terminal. 10,000+ lines of pure C. No libraries. No frameworks. Just ANSI escape codes and math.h.
Python · 0 watchers
cellular-automaton-sandbox
A terminal-based simulation suite featuring 27 interactive modes — from Conway's Game of Life to fluid dynamics, fractal explorers, and 3D ray casting. All rendered in your terminal using curses.
Python · 0 watchers
cellular-automaton-simulator
A single-file Python implementation of cellular automata that runs in the terminal using curses. No external dependencies.
Go · 0 watchers
chat-with-multiple-llms
0 watchers
CHI22-CogMod-Tutorial
CHI 2022 Modeling tutorial is a set of Python Jupyter Notebooks designed as an introduction to cognitive, neural and RL modeling in Human-Computer Interaction.
0 watchers
codesign-test
testing automatic code signing
HTML · 0 watchers
consent
Informed Consent Generator
Go · 0 watchers
cyclemod
enable import cycle using modules?
Go · 0 watchers
demos
code for demonstration purposes
PHP · 0 watchers
destrictor
an SVN-based Web CMS
0 watchers
DGEMO
[NeurIPS 2020] Diversity-Guided Efficient Multi-Objective Optimization With Batch Evaluations
0 watchers
driving-license-de
Get driving license in Germany without a word of German (GGG).
Go · 0 watchers
dummydep
a dummy dependency
0 watchers
ebiten
A dead simple 2D game library for Go
Jupyter Notebook · 0 watchers
expertise-loop
IUI23: Full Paper "The Impact of Expertise in the Loop for Exploring Machine Rationality"
0 watchers
fonts
Patched fonts for Powerline users.
0 watchers
fyne-proposals
Proposals that we are working on for future releases
Go · 0 watchers
ghtest
test gh
Go · 0 watchers
gio
Mirror of the Gio main repository (https://git.sr.ht/~eliasnaur/gio)
0 watchers
go-mpi
MPI bindings for go.
Go · 0 watchers
gomobile
[mirror] Go on Mobile
0 watchers
GPyOpt
Gaussian Process Optimization using GPy
Python · 0 watchers
haggles
My Kaggle Solutions
JavaScript · 0 watchers
hexo-generator-restful
Generate RESTful json data for Hexo plugins.
Go · 0 watchers
ideas
Idea ingestion pipeline to https://changkun.de/blog/ideas/
TypeScript · 0 watchers
LibreChat
Enhanced ChatGPT Clone: Features Agents, DeepSeek, Anthropic, AWS, OpenAI, Responses API, Azure, Groq, o1, GPT-5, Mistral, OpenRouter, Vertex AI, Gemini, Artifacts, AI model switching, message search, Code Interpreter, langchain, DALL-E-3, OpenAPI Actions, Functions, Secure Multi-User Auth, Presets, open-source for self-hosting. Active project.
Go · 0 watchers
mailbot
A regular email sender because of Bundesnotbremse.
Jupyter Notebook · 0 watchers
MasterThesisHCI
Master Thesis for Human-Computer Interaction
0 watchers
media-prospective-memory
CHI23 Full Paper "Short-Form Videos Degrade Our Capacity to Retain Intentions: Effect of Context Switching On Prospective Memory"
JavaScript · 0 watchers
munich-renting-tool
A housing location visualization tool for munich.
0 watchers
NeuroKit
NeuroKit2: The Python Toolbox for Neurophysiological Signal Processing
Dockerfile · 0 watchers
nginx-autoindex
nginx:stable-alpine but enables audoindex
Go · 0 watchers
null-codex
ai-driven repository
0 watchers
o
personal deterministic automation control plane
Go · 0 watchers
oblivion
Experiment: Generating Code Project from Absolute Zero without Goal-specification
 |
oulongqiV2EX member #95220, joined on 2015-02-01 23:31:51 +08:00 |
changkun.de
changkun
changkun
| 使用 M1 两个月来第一次遇到的自动黑屏重启 Apple • oulongqi • Mar 25, 2021 • Lastly replied by sicecake | 5 |
| Airpods Max 的低功耗模式为什么只能在放入耳机套中才能启用？ Apple • oulongqi • Jan 2, 2021 • Lastly replied by snachx | 1 |
| iOS 14.2 上滑返回桌面粘滞感严重？ Apple • oulongqi • Nov 8, 2020 • Lastly replied by chodomatte | 7 |
| MacBook 12 已经停产了都不能参与 GiveBack，苹果想干嘛 Apple • oulongqi • Jul 14, 2019 • Lastly replied by 20015jjw | 9 |
| 分享一下顶配 MacBook 2017 使用一周后的感受 Apple • oulongqi • Jan 30, 2019 • Lastly replied by MadHouse | 57 |
| 预览 Preview 会随着系统升级变得越来越容易 Crash？ Apple • oulongqi • Jun 19, 2017 • Lastly replied by AnyISalIn | 11 |
| 有没有准备入手 2017 款 MacBook 12 的朋友? 为啥感觉关注度不高呢? Apple • oulongqi • Jul 17, 2018 • Lastly replied by zzii | 43 |
| 这次 WWDC 到底升不升 MacBook 12 的配置呢 Apple • oulongqi • May 31, 2017 • Lastly replied by evilangel | 23 |
| 大家觉得什么时候能有 MacBook 12 的更新? Apple • oulongqi • Mar 22, 2017 • Lastly replied by neutron | 23 |
| 想买一台开发本，现在入 Surface 或 MacBook 靠谱吗? Surface • oulongqi • Oct 7, 2016 • Lastly replied by BXIA | 56 |
oulongqi's recent replies
Nov 8, 2020 Replied to a topic by oulongqi › Apple › iOS 14.2 上滑返回桌面粘滞感严重？ |
@chodomatte 正式版问题依然存在
Sep 10, 2019 Replied to a topic by ufo22940268 › macOS › 各位有碰到过触控板回退手势失效的情况吗 |
经常发生 经常重设 蠢材吧无解
Jul 14, 2019 Replied to a topic by oulongqi › Apple › MacBook 12 已经停产了都不能参与 GiveBack，苹果想干嘛 |
@mzdblsw8 人在国外。。
Jul 8, 2018 Replied to a topic by finian › 云计算 › 阿里云上个月的事故赔付明细已经更新了 |
妈的狗屎 阿里云 API 服务全部挂了 赔付方案呢
Sep 26, 2017 Replied to a topic by jamfer › Android › 不考虑价格的话，你最推荐的安卓机是哪部 |
论生态，你没得选，除了苹果，国内只有小米了。当然如果你只想买个手机当我没说，但是你如果只想买个手机，就别如坑安卓了。
论潮流，最新款：MIX2 or Mi 6
论稳重，性价比+够用：Mi Note2 4+64 最近在打折清库存，只需 2k，表示用的很爽。
论潮流，最新款：MIX2 or Mi 6
论稳重，性价比+够用：Mi Note2 4+64 最近在打折清库存，只需 2k，表示用的很爽。
事情是这样的：
曾今有个学派叫做毕达哥拉斯学派，他们信奉万物皆整数或整数之比（有理数）。后来有个不听话的学生质疑他们这个学派的观点，说：『老大，我发现边长为 1 的正方形的对角线不能写成整数或者整数的比，怎么办？』后来他老大（毕达哥拉斯）就火了，一怒之下把这个学生就给弄死了。后来越来越多的人发现好像这个学生是对的，那就是有理数没办法挤满整个数轴，有理数之间还有大量的缝隙（现代的测度论观点证明了有理数集的测度为 0，也就是说有理数的数量和无理数比起来根本不值一提），于是就为无理数正了名。后来逐步证明了当有了 无理数 之后，有理数+无理数能够密密麻麻的挤满整个实数轴，万事大吉。
然后时间来到了十七世纪，一群爱搞事数学家（笛卡尔、欧拉、高斯等）发现，为什么要局限于一根数轴上呢，我们可以往平面上搞事。于是发明了复数，再后来哈密尔顿在有提出了四元数（四维），当然这些都是后话了。
曾今有个学派叫做毕达哥拉斯学派，他们信奉万物皆整数或整数之比（有理数）。后来有个不听话的学生质疑他们这个学派的观点，说：『老大，我发现边长为 1 的正方形的对角线不能写成整数或者整数的比，怎么办？』后来他老大（毕达哥拉斯）就火了，一怒之下把这个学生就给弄死了。后来越来越多的人发现好像这个学生是对的，那就是有理数没办法挤满整个数轴，有理数之间还有大量的缝隙（现代的测度论观点证明了有理数集的测度为 0，也就是说有理数的数量和无理数比起来根本不值一提），于是就为无理数正了名。后来逐步证明了当有了 无理数 之后，有理数+无理数能够密密麻麻的挤满整个实数轴，万事大吉。
然后时间来到了十七世纪，一群爱搞事数学家（笛卡尔、欧拉、高斯等）发现，为什么要局限于一根数轴上呢，我们可以往平面上搞事。于是发明了复数，再后来哈密尔顿在有提出了四元数（四维），当然这些都是后话了。
Aug 16, 2017 Replied to a topic by mritd › Apple › appid 切换美区 1 个月后所有已购被清空 |
不知道你们为什么都把美区当做唯一目标，欧洲不也挺好吗
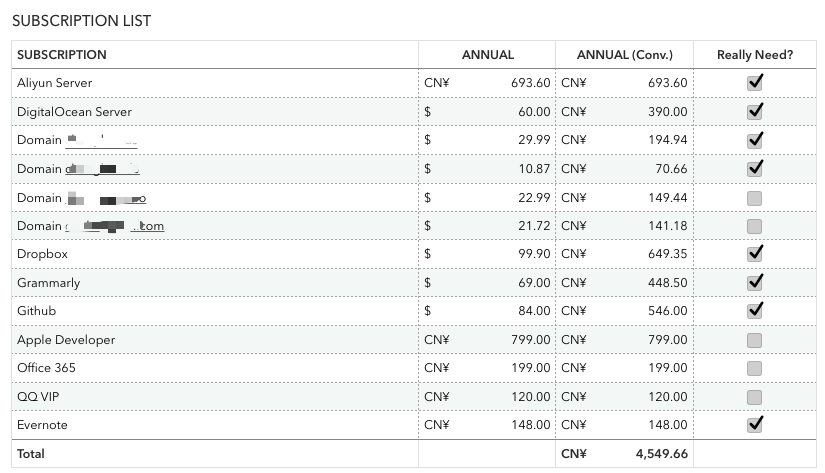
Aug 14, 2017 Replied to a topic by richardad › Apple › 总结了一下自己目前订阅的所有服务，以后订阅的软件越来越多了 |
@ZengLeiPro Numbers
Aug 14, 2017 Replied to a topic by richardad › Apple › 总结了一下自己目前订阅的所有服务，以后订阅的软件越来越多了 |
)
真糟糕...稍微加了一下每年就是 5k 左右的开支..
)真糟糕...稍微加了一下每年就是 5k 左右的开支..
Select Language