这是一个创建于 1308 天前的主题，其中的信息可能已经有所发展或是发生改变。
如图所示，我有 n 个离散的点，一根直线从上方掉落，直到落到“最高”的两个点，（其实不一定是最高，就是这根直线无法再下落，重力势能最小了），然后根据这两个点求得直线方程。
想问下各位大帅逼 /大漂亮用什么算法，或者这个算法的关键词我自己搜索也行，十分感谢。
第 1 条附言 · 2021-04-23 10:21:56 +08:00
点的数量是有限的，偶数个的（比如 50 个），线的定义域跟点的定义域一致。所以线不是无限长的。
我思考了一下，应该是左边 25 个点选一个端点，右边 25 个选一个端点，这样比较符合现实中，用直尺检测地面平整度的物理意义。
所以有位帅哥说的 1 2 2 1 我认为应该取 2 2 而不是 1 2 或者 2 1.
我思考了一下，应该是左边 25 个点选一个端点，右边 25 个选一个端点，这样比较符合现实中，用直尺检测地面平整度的物理意义。
所以有位帅哥说的 1 2 2 1 我认为应该取 2 2 而不是 1 2 或者 2 1.
 |
1
HaydenYe 2021-04-23 09:34:02 +08:00
先找最高点 然后绕最高点旋转？ 第一次相交情况就是吧（顺逆时针都可以 然后取低值）
|
 |
2
Raven316 2021-04-23 09:35:10 +08:00
所以图呢。。
|
 |
4
marcong95 2021-04-23 09:40:22 +08:00
找出来两个极值连一条线？
不过这个重力势能是不是有点难定义，例如我在两点直接直接戳一条平行于 y 轴的直线，那算不算？ |
 |
6
codehz 2021-04-23 09:41:49 +08:00 via Android
这样描述的话，听起来会有很多边界问题，怎么判定最高，举个例子
4 个数据点 2 4 1 2 是选择 1 2 点连线还是 2 4 点呢 |
 |
7
lance6716 2021-04-23 09:42:19 +08:00 via Android  1
凸包
|
 |
8
ly90907 OP @Raven316 啊，看不到吗？我还专门预览过 https://imgur.com/ntO2HZS
@HaydenYe 我想过，假设右边有两个挨着的同样值的最高点，用你说的旋转只会是这两个点通过的直线，但是我需要的是橘色的线 ) |
 |
9
inertia 2021-04-23 09:45:27 +08:00 2
这条线可以这么定义，在点集中取两个点，将其连成一条直线，点集中的除这两个点外的所有点都在直线之下
|
 |
10
Stoulla 2021-04-23 09:45:51 +08:00 via Android
7 楼应该是正解，这玩意儿就是找一个凸包
|
|
11
ly90907 OP @codehz 就是类似于不平整的地面上放一根直尺，我想测量离尺最远的地面的距离，当然如果地面是突起的，那我觉得应该就是地面中心做切线吧
|
 |
13
ynyounuo 2021-04-23 09:48:12 +08:00
我觉得如果直线是无限长度的，那么落点必然是两个 local maxima，用 scipy 的 find_peaks 找两个最高点，两点求方程就不用说了吧
|
 |
14
Mithril 2021-04-23 09:49:24 +08:00
你这个本质上是在计算凸包的一条边。先把凸包算出来就好了。
|
 |
15
ryd994 2021-04-23 09:50:33 +08:00 via Android
这个解可能不唯一啊
如果是 1 2 1 那么有两个解 如果是 1 2 2 1 那么可以有三个解 |
 |
16
sujin190 2021-04-23 09:53:13 +08:00
搞不懂这个的问题难点在哪，楼主既然已经画了二维平面，那么直线下落到最高的必然是所有数据中两个最大值上啊，没有其他情况了吧，两个点确定一个方程组这种小学应用题还用来问啊
|
 |
17
Vinty 2021-04-23 09:53:50 +08:00
遍历一遍局部峰值点，找全局最高点，然后搜索局部峰值
假设峰值点的集合为 d = {X,Y}, 最高点和其中一条峰值点的直线为 ax+b 所有的 aX+b > =Y 时，就是满足条件的解。搜索方法应该还能再改进，暂时没想到 但是，如果是这样的，会有两个解  |
 |
18
GuuJiang 2021-04-23 09:54:18 +08:00 via iPhone
首先你得定义整个范围的左右边界，找出其中点 m，然后找到 y 最大的点，如果 m 在其左侧则逆时针旋转，在右侧则顺时针旋转，找到下一个碰到的点，如 m 介于两点的 x 之间，则中止，者两点就是所求，否则 m 必然位于两点同侧，那继续在哪侧就像哪侧旋转，重复直至 m 位于两点之间
|
|
19
Mithril 2021-04-23 09:54:19 +08:00
算凸包的时候加上两个点，（ 0,0 ）和（ max_x, 0 ），算出来的凸包去掉那三条固定的边，然后剩下的边里面挑个斜率最接近 0 的就行了。
|
 |
20
whileFalse 2021-04-23 09:56:03 +08:00
题目有问题，因为无法比较两条 [直线] 的重力势能。如楼上的 1,2,2,1，如何比较 1，2 和 2，2 的重力势能哪个大？
|
|
22
Mithril 2021-04-23 10:03:28 +08:00
忽然发现你这题目确实有问题。。。如果是无质量的直线那么它必然过最高点。
但如果按你说的，可能如果不过最高点，就按你说的根据重力势能算，那就得考虑重心问题，它就不可能是直线。。。 @ly90907 比如你 8L 第一张图，如果右侧两个最高点之间的距离很远，那么蓝色线就是对的 |
|
23
GuuJiang 2021-04-23 10:03:53 +08:00 via iPhone
@GuuJiang 这题要有解，两侧必须是有界的，换句话说你想求的其实不是“直线”，而是线段，否则的话就以你在#8 发的那个反例来说，最开始的两个点在图里看起来不满足，但是只要往右边延伸足够长度，又变成满足的了，继续往右延伸，再次变成不满足，且正解变到了它们的右侧，所以必须要先定义范围
|
 |
24
zxCoder 2021-04-23 10:20:11 +08:00
直线没办法
线段感觉稍微有点复杂，得看怎么定义这个重力势能 |
 |
26
stonewolfcjq 2021-04-23 10:27:31 +08:00 via Android
找个最高点，再依次计算最高点和其他每一点连线的直线斜率，取绝对值最小的那个
|
|
27
GuuJiang 2021-04-23 10:37:17 +08:00 via iPhone
其实就是先求上凸包，然后在构成上凸包的各线段中取包含 m 的，必然会有一段或两段，如果只有一段即为所求，如果有两段说明 m 是它们的交点，此时结果取决于定义
|
 |
28
chairuosen 2021-04-23 10:40:19 +08:00
9L 正解吧
|
 |
29
Jirajine 2021-04-23 10:55:37 +08:00 via Android
按你的说法，首先假设线段长度远大于点的定义域 /值域范围，线段重心正好在定义域中点上下落。线段与点之间不考虑滑动（摩擦系数视为无限大）。
那么很简单了，首先最高点一定能取到，先取到最高点以后向线段重心所在方向旋转，碰到第一个点停止。判断重心是否在两点之间，如果不在就放弃第一个点，绕第二个点继续向重心方向旋转，直到重心在两点之间为止。 |
 |
30
aneureka 2021-04-23 13:38:07 +08:00
@Jirajine #29 不一定能取到最高点吧，比如这种情况，绿线应该才是正解
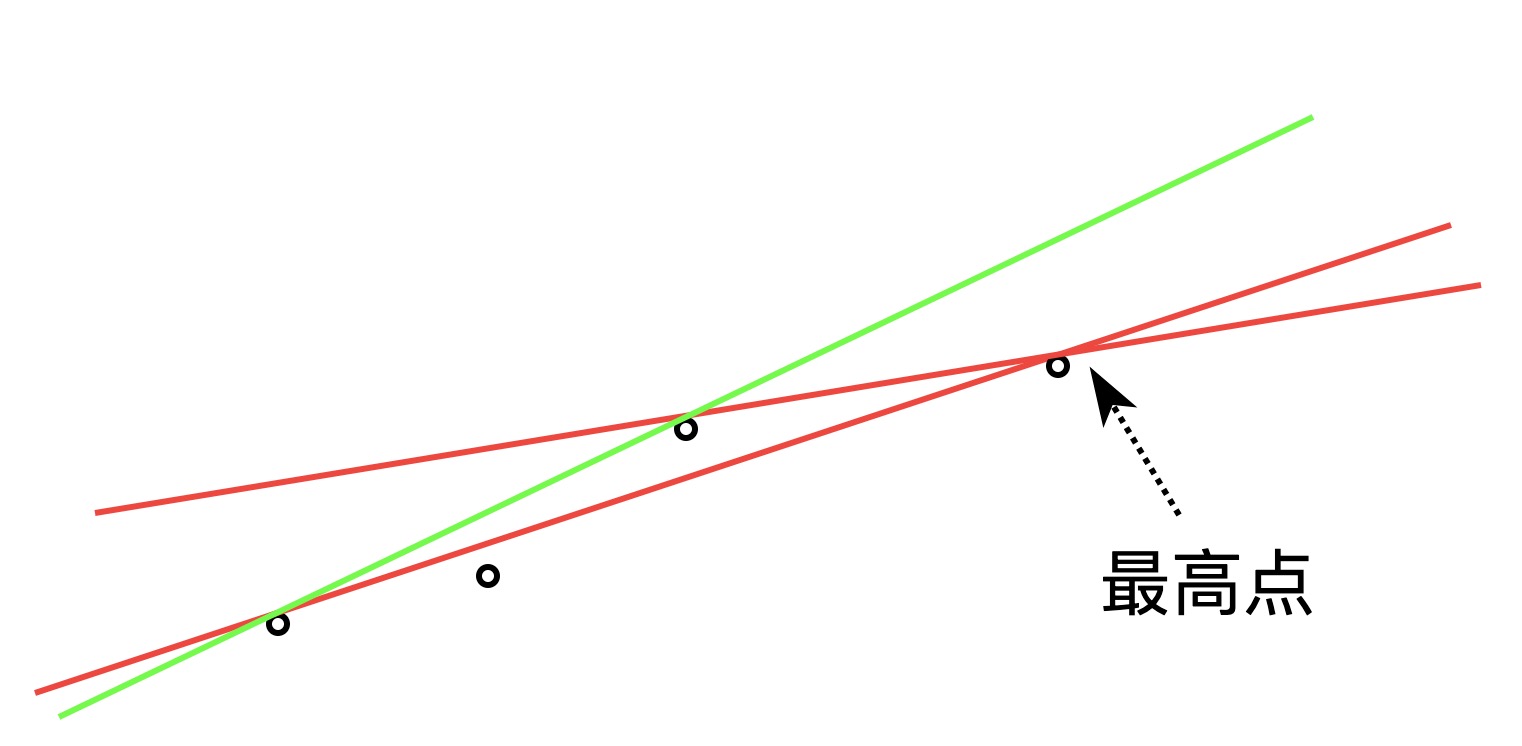 （不知道图片能不能正常显示） |
 |
31
ho121 2021-04-23 13:46:03 +08:00 via Android
点不多的话，用穷举？
|
|
32
Jirajine 2021-04-23 13:51:48 +08:00
@aneureka #30 你没有看完我写的，假设是水平下落，第一个碰到的点一定是最高点。判断重心后再旋转。本质上是模拟下落的过程。
|
 |
33
L5411 2021-04-23 13:51:58 +08:00
必须得计算线段的重力势能吧
|
 |
36
3dwelcome 2021-04-23 14:01:30 +08:00
|
 |
37
oamu 2021-04-23 15:40:54 +08:00
找一条直线，其他点都在这条直线下面？那不是找出最大的两个值，两点式一算就出来了么。
|
|
39
aneureka 2021-04-23 16:04:18 +08:00 via iPhone
@3dwelcome #35 哈哈确实 感觉还是得根据实际情况来 这个问题定义感觉不是太严谨 其实点不多的话用个 On^3 的循环扫一遍也就可以了
|
|
40
GuuJiang 2021-04-23 17:10:32 +08:00
总结下，首先“其他所有点都在直线之下”这个只是必要非充分条件，因为上凸包里的每一段所在的直线都是满足这个条件的，所以问题转化成了求上凸包里某一段所在的直线，关键在于这一段应该满足什么条件，上面有不少人说一定过最高点的，还有说斜率最小的，这两个都是不对的，反例都已经在#8 的图里给出来了
其实 LZ 你最开始描述问题的方式已经非常接近真相了，想象下这个物理过程，线落下来接触了一个线段以后为什么还会旋转，就是因为中心落在了线段之外，所以所求线段需要满足的条件已经很明显了，就是让重心落在内部，由于假设是质量均匀直线，所以重心自然就是中点(PS：就算题目换成质量不均匀的线段也可以用同样的方法求解，只需要换成真正的重心即可) 另外，相比起传统的求上凸包方法，针对这个问题可以做一些优化，起点只需要从最高点开始，并且根据重心位置只用考虑它的一侧，另一侧直接丢弃，另外过程中只需要碰到第一个包含了重心的线段就可以停止了，因为重心只可能包含在一个线段内（在交点的情况忽略） |
 |
41
lidlesseye11 2021-04-23 17:20:52 +08:00
感觉楼主想要的是个类似于豪斯多夫距离的概念？
满足 9L 描述的有不止一条直线，定义 Di 为点 i 到直线的距离的话，楼主想要的是使 max （ Di ）最小的那条线？ |
 |
42
shyrock 2021-04-23 17:22:48 +08:00
1.下落到最高点，如果最高点多于 2 个，则解是连接这两个点的直线。
2.如果最高点只有一个，则判断最高点在左侧还是右侧，然后以最高点为原点，对侧的点按极坐标排序，第一个扫到的点和最高点确定直线 |
|
43
lidlesseye11 2021-04-23 17:23:13 +08:00
@lidlesseye11 又或者是使 sum （ Di ）最小的那条线？
|
 |
44
akira 2021-04-23 19:45:39 +08:00
找到最高点
以最高点为原点建立极坐标 扫描两侧的点 所以应该是有 2 个解... |
 |
45
rus4db 2021-04-23 20:00:37 +08:00
关键词：凸包算法
|
 |
46
wa007 2021-04-24 08:41:00 +08:00 via iPhone
找到最高点，最高点肯定经过这条直线，然后遍及其他点，与最高点连成一条直线，斜率绝对值最小的直线就是答案
|
 |
47
LxExExl 2021-04-24 13:59:55 +08:00 via iPhone
楼主如果是炒股我觉得技术分析啥的都没用
各种均线看看就行了 还是选成长股优质股然后长线定投 |
 |
48
oylinv 2021-04-24 16:37:12 +08:00 via iPhone
这个的话，最简单的方法，就是按顺序取两个点，用这两条点建立直线，再判断其他点是否在这条线下方（点到直线距离公式去掉绝对值）， 如果存在上方的点，则顺序换接下来的两个点计算。
就是计算次数比较多 |
|
49
ly90907 OP 感谢各位的回复和解答，由于人数较多就不一一回复了，看了各位的回答，并且思考 @GuuJiang 和 @Jirajine 这两位朋友的回复就是我想要的答案。并且整理了一下，写了一个总结。https://zhuanlan.zhihu.com/p/367706616
懒得点的话我就直接把伪代码贴上，以供分享。 遍历点集找出最高点 P1 ； if P1∈[0，N ） 遍历 P1 右边的点，计算斜率 k，找出 k 最大的点 P2 ； if P2∈[N，2N ） 得到 P1，P2 为最终结果 else P1 = P2， 递归上述过程 else if P1∈[N，2N ） 遍历 P1 左边的点，计算斜率 k，找出 k 最小的点 P2 ； if P2∈[0，N ） 得到 P1，P2 为最终结果 else P1 = P2， 递归上述过程 @sujin190 @ryd994 @Vinty @whileFalse @zxCoder @stonewolfcjq @aneureka @ho121 @3dwelcome @oamu @shyrock @wa007 @LxExExl @oylinv |
|
50
ryd994 2021-04-25 17:21:07 +08:00 via Android
既然反正是 O(n^2)
那直接遍历经过每每两点的直线，使得直线在 1/2 处的值最大化即可 这样做虽然计算量大一点，但是可以很容易并行化 |
Select Language