这是一个创建于 1158 天前的主题，其中的信息可能已经有所发展或是发生改变。
比如
verts = [(x0,y0),(x1,y1),(x2,y2),(x3,y3)]
怎样保证能创建这样的面
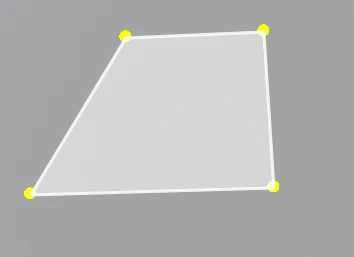
而不是这样
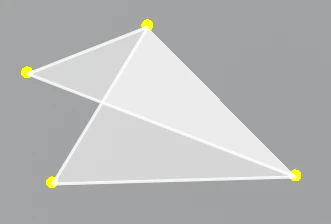
要求这四个点坐标不变，最小限度修改前 3 个点的下标（顺序），逆时针，否则面法线就会朝内，最后一个点不能动？ 有什么好办法吗？
 |
1
vance123 2021-09-22 23:07:56 +08:00 via Android
以最左下方的点为原点，算出三个向量和 y 轴正向的夹角，然后排序
|
|
2
vance123 2021-09-22 23:23:21 +08:00 via Android
不过只有既然四个点，枚举然后像你说的那样算法线方向也可以
|
 |
3
IgniteWhite 2021-09-22 23:29:40 +08:00 via iPhone
|
 |
4
MoYi123 2021-09-23 09:32:36 +08:00
|
 |
5
XiXiLocked 2021-09-23 13:12:25 +08:00
比叉乘，(p1-p4)x(p2-p4) ，(p3-p4)x(p2-p4) ，轮换 123 。3 次里会出现一次一正一负，用那次的下标绕 1234 就不会重叠。
|
 |
6
necomancer 2021-10-23 16:02:53 +08:00
from scipy.spatial import ConvexHull
hull = ConvexHull(verts) # 你的例子里 points = (4,2) array ，一般来说数组形状是（点数，维度） 剩下的看看 hull 的 vertices 就行，这个是寻找平面最大凸多边形算法，详情查书。 当然，如果你的 4 个点里有一个藏在内部了，这个算法返回的是三角形。比如你的 4 个点这么排列，那么返回的是外面的三角形。 * ----*----* * |
Select Language