这是一个创建于 2063 天前的主题，其中的信息可能已经有所发展或是发生改变。
如下图所示，实线为可通行路线，虚线和 X 为不可通行路线。其中 CDGH 为正方形，CH 和 HG 中只有一条为实线，每隔 30 秒实线和虚线互换一次，CD 和 DG 同理，CDGH 中的实线始终保持平行状态，可以理解为十字路口的红绿灯。
小明需要从 A 点走到 E 点，现在有两种方案
1. 沿着 ABCDE 走，只过一次红绿灯
2. 沿着 AHDE 走，过两次红绿灯
遇到红绿灯的时机不确定，那么问题来了，这两种方案那个花费的时间更短？还是说两种方案时间一样？
小明需要从 A 点走到 E 点，现在有两种方案
1. 沿着 ABCDE 走，只过一次红绿灯
2. 沿着 AHDE 走，过两次红绿灯
遇到红绿灯的时机不确定，那么问题来了，这两种方案那个花费的时间更短？还是说两种方案时间一样？
 |
1
Biwood OP 咦？没人看吗，我琢磨着可以写个程序算一下平均值什么的
|
 |
2
craiiz 2019-03-25 21:55:35 +08:00 via iPhone  1
小明很累的....
|
 |
3
takato 2019-03-25 22:01:25 +08:00
时间是如何度量的？
走过一条边+x 秒？还是有特殊的计量方法？ |
 |
5
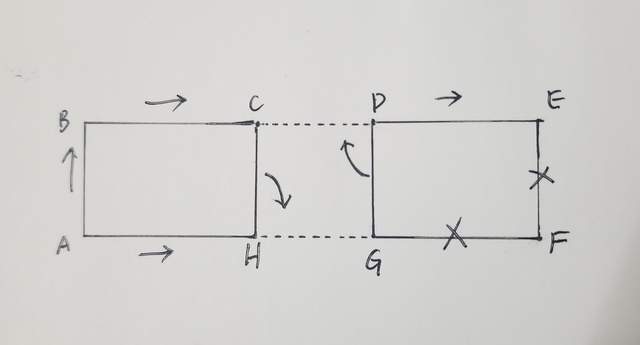
SuperMild 2019-03-25 22:17:20 +08:00 1
假设 AB 30 秒，BC 60 秒：
1. ABCDE，运气最好的时候无需等灯，30+60+30+60 = 2min，运气最差的时候等 30 秒，即 2:30 2. AHCDE, 运气最好的时候无需等灯，30+60+30+60 = 2min，运气最差的时候等 30+30 秒，即 3min |
|
6
Biwood OP @SuperMild 方案二应该不会出现 30+30 的情况，因为他走到路口的时候总会又一个是绿灯，HC 行不通的时候，HG 肯定行得通
|
|
7
SuperMild 2019-03-25 22:35:35 +08:00
@Biwood 即使能通行，但如果下一秒就到了虚实转换的时间，就不够时间过去了，假设 HC 的路程也要走 30 秒，如果 15 秒后就到转换时间，也过不去。
总之这题就算一个最佳情况和一个最坏情况，条件随你怎么变，比如你假设小明可以秒过，那 2.AHDE 的最好和最差就和 1 一样，不能比 1 更好。 |
|
8
takato 2019-03-25 22:50:45 +08:00
|
|
9
Biwood OP @takato 30s 是为了标识转换的间隔时间是相等的，也可以写成“固定时间”。当然，为了方便理解，可以给出具体的数字，比如红绿灯每隔 30s 变换一次，走过 AB 需要 10s，走过 BC 需要 20s，以此类推。
|
 |
10
qwertyegg 2019-03-26 01:50:30 +08:00
几何分布问题，这两条路径的期望时间是一样的
|
 |
11
widewing 2019-03-26 02:53:08 +08:00 via Android
小明的速度呢？走到一半变线的情况？
|
 |
12
ihciah 2019-03-26 05:46:51 +08:00 via iPhone
ABCDE 相当于一半常绿的红绿灯，期望上更优
|
 |
13
Elethom 2019-03-26 06:33:52 +08:00 via iPhone
数学期望问题，这跟算法有什么关系。
|
 |
14
binux 2019-03-26 07:13:23 +08:00 1
我猜一个，当你过马路时间小于 (√2 - 1) 倍亮灯时间的时候，1 快，否则 2 快
|
|
15
Biwood OP @widewing 就排除掉走到一半变线的情况吧，假设小明总是能在绿灯期间过去。速度是固定的，可以不用管，只需要根据时间和概率来推理即可。
|
|
16
Biwood OP @ihciah 为什么我觉得方案二期望更优先呢，你想想，方案一小明运气最差时要等完 30 秒，而方案二中，小明过第一个红绿灯的时候，第二个红绿灯相当于已经等待一段时间了，他好像永远不需要等完 30 秒。
|
|
17
binux 2019-03-26 07:54:59 +08:00
@Biwood #16 你 #15 的「小明总是能在绿灯期间过去」和「第二个红绿灯相当于已经等待一段时间了」根本就是矛盾的。既然第二个绿灯已经等待一段时间了，那么这段时间小明过的第一个路口是红灯啊！除非小明是闪电侠。
|
|
18
Biwood OP @binux 我写的是“第二个红绿灯”而不是“第二个绿灯”。举个例子，小明过第一个绿灯 HC，这时候 CD 肯定是红灯吧，又或者过第一个绿灯是 HG，那这时候 GD 肯定是红灯吧。每当过完第一个绿灯，第二个路口的红灯已经过去一段时间了，不需要等待 30 秒才变绿灯。
|
|
19
binux 2019-03-26 08:12:36 +08:00
@Biwood #18 我 #14 通项都给你算好了，是否节省取决于过马路的速度，即黄灯的时间比例。你所谓「方案二期望更优先」完全建立在小明走一半变红灯，别人让他的情况下。
|
 |
21
geelaw 2019-03-26 08:19:22 +08:00 via iPhone 1
假设看起来相等的线段相等，小明在小于 30 秒内的时间可以通过红绿灯的一边，不需要考虑转弯的时间，开始时间是在红绿灯周期（ 60 秒）的均匀分布，则显然是只过一次红绿灯期望时间小。
利用耦合法：考虑两个平行世界，它们的红绿灯情况相差通过 AB 需要的时间，世界 X 走第一条路，世界 Y 走第二条路。在 Y 中可以通过 CD 或 GD 时（最后一个红绿灯路），在 X 里更早或当时也可以通过 CD。 |
 |
22
hearfish 2019-03-26 08:20:03 +08:00 1
就假设他通过的时间忽略不计（远小于 30 秒）
方案一：最多等 30 秒，最少等 0 秒，平均等待 0.5 * 0 + 0.5 * 15 = 7.5 秒 方案二：无论哪边是绿灯，他都瞬间通过，下一个一定是红灯，平均：15 秒 考虑他通过的时间，假设他需要 10 秒过马路，红绿灯上有倒计时，且他只在绿灯倒计时超过 10 秒时过马路 方案一：最多等 40 秒（小于 10 秒的绿灯 + 30 秒红灯），最少等 0 秒，平均 0 * 1/3 + 20 * 2/3 = 13.3 秒 方案二：到路口时有两种情况 1. 绿灯不到 10 秒：等另一个红灯变绿，通过后继续等 20 秒红灯，平均：5 + 20 = 25 秒 2. 绿灯大于 10 秒：通过后下一个一定是红灯（最多 20 秒），平均 10 秒 总平均：25 * 1/3 + 10 * 2/3 = 15 秒 同样假设他要 10 秒过马路，如果没有倒计时，他过马路的时候红绿灯智能维持绿灯状态，直到他过完马路（即绿灯状态最长可达 40 秒） 方案一：平均等待 0.5 * 0 + 0.5 * 15 = 7.5 秒 方案二 1. 绿灯不到 10 秒：直接通过，下一个一定还是绿灯，平均 0 秒 2. 绿灯大于 10 秒：通过后下一个一定是红灯（最多 20 秒），平均等待 10 秒 总的平均等待时间：0 * 1/3 + 10 * 2/3 = 6.7 秒 至于通项，把 10 秒换成 X，解一下不等式就完事了 |
|
23
hearfish 2019-03-26 08:24:26 +08:00
什么？你说红绿灯既没有倒计时也不智能？行人闯红灯好像也是全责吧🐶
|
 |
24
w2cny 2019-03-26 08:28:37 +08:00 via Android
脑子不够用，@-@
|
|
25
binux 2019-03-26 08:30:05 +08:00
@hearfish #23 怎么可能有智能红绿灯嘛，按照中国这个情况，10 秒内一定还会有人开始过马路啊，那就是无限绿（红）灯啊。
|
 |
26
autoxbc 2019-03-26 23:26:54 +08:00 1
这个从红绿灯得到的灵感，那么应该遵守红绿灯的规则
1. 红绿灯周期为 2t (变绿 => 变红 => 变绿) 2. 绿灯可过，中间变灯可继续通过 3. 行人通过时间为 x，按照常识 x < t 单个红绿灯 绿灯半周期 t，等待时间为 0 红灯半周期，等待时间从 0 ~ t 整个周期的等待时间期望为 4/t 两个连续的随机红绿灯等待时间期望 ( 4/t ) * 2 = t/2 正方形的十字路口 因为总有一边为绿灯，第一个灯的等待总是 0，则总等待就是第二个灯的等待 进入路口为绿灯开头：等待时间 t - x 进入路口为绿灯中间某点，过第一灯刚好切信号，等待时间 0 进入路口为绿灯末尾：等待时间 0 这是个线性下降曲线，期望为曲线围出的三角形在 t 上的均值 ( t - x )^2/(2t) 这是个抛物线，在 y 轴有 t/2 截距，顶点在 x 轴 ( t , 0 )，开口朝上，左半边取值有效 (因为 x < t ) 由此可知，当行人通过时间等于半周期时 ( x = t )，等待期望为 0，由于等待不能为负值，所以等待必为 0 因为截距为 t/2，故斜穿十字路口(4 个信号正交的信号灯)，永远比通过两个连续的随机信号灯要快，即行人因为多了一组路径，人为选择后必然节省时间 注意到单个灯的期望为 t/4，则回到题目，方案 1 & 2 的期望需要由 x 和 t 的关系算得 令 ( t - x )^2/(2t) = t/4，解出临界点为 x = ( 1 - 1/√2)t ≈ 0.2929t 当行人速度很快，x < 0.2929t 时，方案 1 更优 当行人速度较慢，x > 0.2929t 时，方案 2 更优 作为特例，当 x 接近 t 时，等待时间为 0 |
 |
27
okface 2019-03-27 13:05:38 +08:00
@binux 老哥，问个 pyspider 的问题哈，project 过多的时候加载任务是有上限的吗，为什么 on_start 方法里一个 150 万行的文件就读了 30 万行进去
|
 |
29
MinakoKojima 2019-04-17 16:47:39 +08:00
14 年多校第二场有一道一模一样的题目，ZCC Love traffic lights。
題意：給一個 20*20 的帶權網格圖，每個結點處有紅綠燈，顏色爲紅 - 綠 - 紅， 綠燈時可以隨便走，紅燈只能右轉，或者闖一次紅燈扣光 12 分，給出綠燈亮起的時間，求 S 到 T 的最短路(到達時間 - 出發時間最短) 解法大概是简化状态 + 最短路。 题目： http://acm.hdu.edu.cn/showproblem.php?pid=4881 题解： http://blog.sina.com.cn/s/blog_6bddecdc0102uyex.html |
Select Language