这是一个创建于 1103 天前的主题,其中的信息可能已经有所发展或是发生改变。
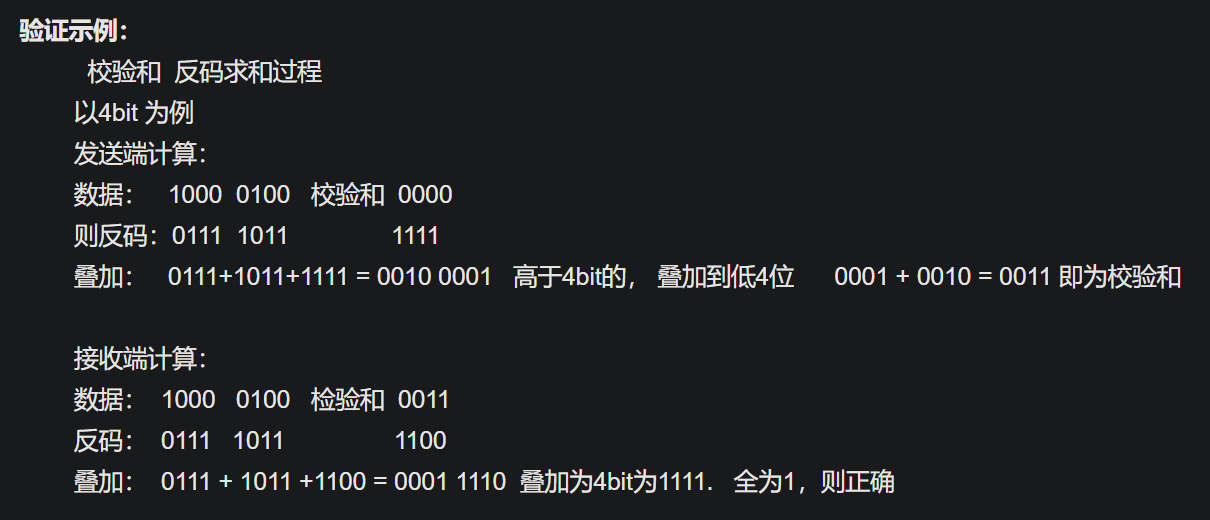
- 就是有点不明白,为啥这么弄了以后,接收方最后算出来就会全是 1 ?(当无比特差错时)(居然最后还有个叠加操作)
unsigned short checksum(unsigned short *buf,int nword)
{
unsigned long sum;
for(sum=0;nword>0;nword--)
sum += *buf++;
sum = (sum>>16) + (sum&0xffff);
sum += (sum>>16);
return ~sum;
}
- 上面这个校验和算法,是先求和,最后取反码,好像也可以(因为算出来是一样的)?这是什么原理(因为上图是 先取反码,再求和,最后叠加。难道这三步 任意换顺序都可以吗)
sum += (sum>>16);这一步看起来是多余的吧?因为上一句就把 前 16 比特 和 后 16 比特 累加了啊?
参考文章:
1
nuk 2021-11-18 00:33:51 +08:00
啥叠加啊,不是求和么,求和就不会是全 1 了啊,2 是考虑到高 16 和低 16 相加溢出的情况
|
2
crab 2021-11-18 01:08:25 +08:00
00001000 (数据 1 )
00000100 (数据 2 ) 00001100 (相加) 11110011(取反 检验和) ------------------ 00001000 (数据 1 ) 00000100 (数据 2 ) 11110011(上面的检验和) 11111111 (相加) |
3
2i2Re2PLMaDnghL 2021-11-18 09:55:58 +08:00
sum = ~X + ~Y + 1111
check = ~X + ~Y + ~sum check = ? 这简单的数学不是很清晰的吗? 至于高 4b 加到低 4b 上去,其实是在模 15 空间内做计算 |
4
qbqbqbqb 2021-11-18 18:28:05 +08:00
所谓的“反码”(英文名是 ones' complement )是一种负数的表示方式,定义上是这样的:
-x = [11..11]2-x = “x 取反” 其中[11..11]2 表示二进制数“w 个 1” 根据上面的定义,不难发现反码加法实际上就是关于 2^w-1 取模的加法。 这样就不难理解为什么计算反码加法要“溢出高位叠加到低位”了:因为平常编程里的普通整数加法溢出时是关于 2^w 取模的,而反码加法是关于 2^w-1 取模,普通加法里低位每向高位溢出一次两者的差值就增加 1 ,所以这样叠加一下算出来的数值恰好是正确的。 原则上应该每加一次就叠加一次,但是因为 IP 头和 TCP 头的字节数不是太长,溢出总数不可能达到 2^16 ,所以说无论先加再叠加还是每加一次就叠加一次,得到的结果没有什么差别。 理解了反码的原理以后,校验和算法就可以一句话描述:每 16 比特当成一个整数,全部相加(包括校验和本身),再除以 65535 (即 2^16-1 )余数应该为 0. |
5
qbqbqbqb 2021-11-18 18:47:36 +08:00
@qbqbqbqb 知道了上面这些之后,不难发现为什么先取反和后取反都是正确的:
如果已知其它数字要求校验和,假设其它数字为 x1,x2,...xn ,校验和为 c ,则根据规则应该满足: x1+x2+...+xn+c=0 (注意这里加号"+"表示反码加法,不是普通加法!) 计算校验和 c 就有两种方式: c=-x1-x2-...-xn (相当于每个数先取反) 或者 c=-(x1+x2+...+xn) (相当于最后取反) 这里关键点就是:“反码运算” 中 “取反”相当于“加负号” 同时也可以发现,接收端其实是没必要取反的。 |
6
qbqbqbqb 2021-11-18 19:08:57 +08:00
@qbqbqbqb 这里唯一一个有问题的地方就是,当校验和为 0 的时候不同的算法可能算出 0 或者 0xffff 两种不同的结果。这两个数字在反码运算里是等价的,但是网络协议上可能有特殊的规定。网络协议里 TCP 没有特别的要求,而 UDP 要求校验和字段算出 0 的时候必须填入 0xffff (全 0 校验和在 UDP 里表示发送端没有计算校验和)。
|
7
amiwrong123 OP @qbqbqbqb #4
正数的话,原码和反码相同。 负数的话,反码是 把负数绝对值的原码,按位取反,再把符号位置为 1 。这样,负数的反码 和 负数绝对值的反码(负数绝对值就是正数,正数的话,原码和反码相同)恰好各个位都是 相反的。 从上可以得知(假设为 4 位 bit 的数)(|负数|是这个负数的绝对值): 负数的反码 + |负数|的反码 = 1111 所以就得出了 ~x = [11..11]2-x = “x 取反” 因为 负数的反码 = 1111 - |负数|的反码 然后你说的“反码加法”就是指两个反码相加是吧。 但我还是没懂“反码加法实际上就是关于 2^w-1 取模的加法”这句话。 比如 负数 a 的反码 = 1111 - |负数 a|的反码 负数 b 的反码 = 1111 - |负数 b|的反码 那么 负数 a 的反码 + 负数 b 的反码 = 1111 + 1111 - |负数 a|的反码 - |负数 b|的反码 但是怎么理解成“关于 2^w-1 取模”啊 有点笨,求指点迷津啦 |
8
amiwrong123 OP |
9
amiwrong123 OP @qbqbqbqb #4
普通的数 的加法里,溢出后,溢出的那一位 刚好就代表 2^w ,所以普通的数 加起来 不用特殊操作。 反码 的加法里,溢出后,溢出的那一位也是就代表 2^w 的,但反码的范围是 [0000-0111 ,1000-1110] (前者 正数,后者负数,-0 么有算在里面),所以就 应该再把溢出那一位 1 加到后面(但这里我 无法正确表述这个道理,希望大佬解释下) 总之,两个反码相加,可能会得到 0001 xyza ,而“溢出高位叠加到低位”就是把这个 0001 ,给加进来。 |
10
amiwrong123 OP @qbqbqbqb #4
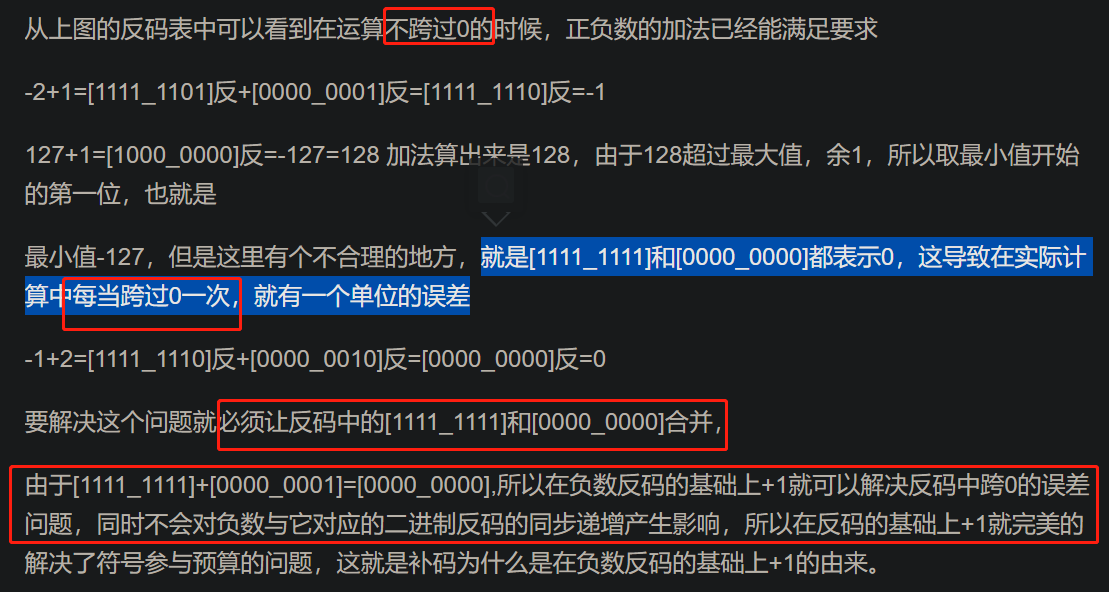 我好像通过这个懂了,为什么 要“溢出高位叠加到低位”。但我好像还是没通过你的这句话,来 get 到为什么“溢出高位叠加到低位”。 哎,我太笨了 总之,不管是再加 1 ,还是“溢出高位叠加到低位”,都是为了 保证 反码 a+反码 b = 反码 c (因为 a+b=c ) |
11
amiwrong123 OP @qbqbqbqb #5
> x1+x2+...+xn+c=0 本贴中第一个图中,发送方的数据是 1000 0100 ,最后算出来的校验和为 0011 , 1000 + 0100 + 0011 = 1111. 为啥我这算出来是 全 1 呢😂,是我哪里理解错了 😂 |
12
qbqbqbqb 2021-11-19 12:15:39 +08:00
@amiwrong123 反码里全 0 表示“+0”,全 1 表示“-0”,数学上可以认为是等价的,是 0 这个数的不同的表示方法。
|
13
qbqbqbqb 2021-11-19 12:27:34 +08:00
@amiwrong123 实际计算中确实是全 1 ,因为计算的过程中不会故意对 2^w-1 取模。
|
14
amiwrong123 OP @qbqbqbqb
大佬,再问一下这个算法: sum = (sum>>16) + (sum&0xffff); sum += (sum>>16); 1. 这两句,我理解后面这句话 sum += (sum>>16);是有必要的,因为前面这句 sum = (sum>>16) + (sum&0xffff);可能又发生了溢出,所以针对这种可能出现的情况,我们需要再做一次 sum += (sum>>16);?是这样理解的吗 2. 但为什么第二句不是 sum = (sum>>16) + (sum&0xffff)呢? |
15
amiwrong123 OP @qbqbqbqb
又或者根本不该加 sum += (sum>>16); |