这是一个创建于 3374 天前的主题,其中的信息可能已经有所发展或是发生改变。
摘要 | 爱好博彩业和投资学的同学应该都对著名的 凯利公式不陌生。这是一个通过计算 edge 和 odds 来选择最佳投注比例的公式,目的是为了追求长期投资获利的最大化,根据赢输的概率及获利多少来决定投资(赌注)的大小。
一:先介绍一下凯利公式: https://uqer.io/community/share/583baaf8228e5b49ef4ac73f
凯利公式的简化公式: f=p-q/b f :投注金额占总资金的比例 p :获胜的概率; q=1-p b :赔率 凯利公式出处原文对赔率的定义: b is the number of dollars returned for a one-dollar bet( including that one dollar). 既然是 bet ,那么 b 是指 bet 后如果赢了拿回的钱,如果输了为 0. 比如,投注 1 元掷骰子,赢了获得 10 元(“不?”包含投入的 1 元),输了为 0 ,则赔率为 10.(实际上就是 r_1=1 r_2=10 f=p/r_1-q/r_2 (这是标准公式)) (注:原文强调是包含投入的一元,但我感觉应该是不包含投入的一元,否则赔率应该为 9)
二:数学上的证明 可以参考这个博客: https://uqer.io/community/share/583baaf8228e5b49ef4ac73f 实际上就是 max(g) _
三:进行模拟实验: 取参数 p=0.6 r_1=1 r_2=1 计算得: f=0.2=0.6/1-0.4/1 初始资金 100 元 , 进行 1000 次赌博,令 f 分别为从 0.1-0.3 (分度值为 100 ) 进行试验。记录 f 值和对应的最后资金大小 和 复合收益率
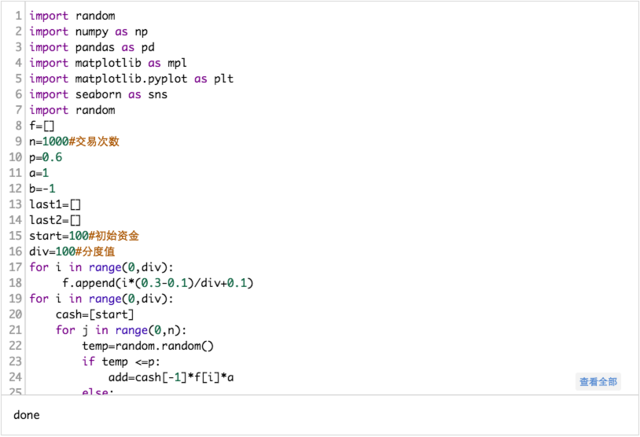
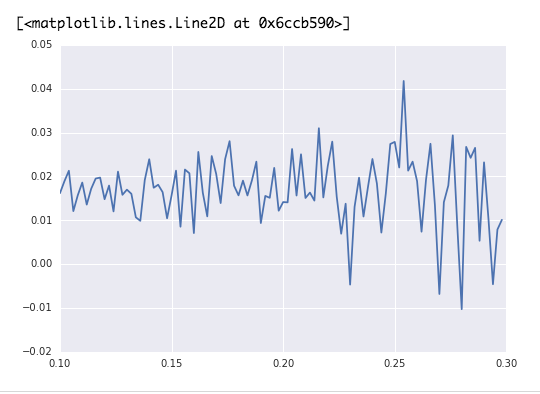
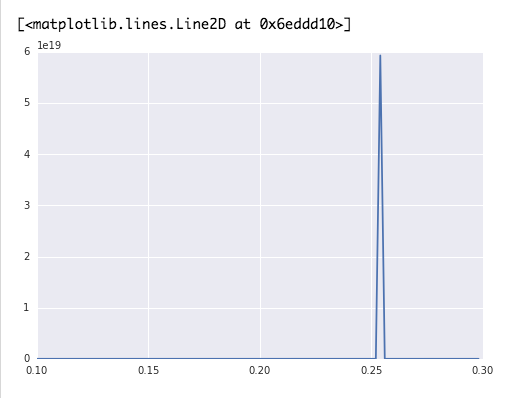
实验分析:修改赌博次数 修改 div 分度值 存在的问题: https://uqer.io/community/share/583baaf8228e5b49ef4ac73f
( 1 ):按道理来讲应该是在 f=0.2 的时候 (确实是平稳随机过程)
( 2 ):混沌效应很明显 (原因可能是由于随机性在其中,对于 f 的微小改变在赌博多次后结果会差别巨大)(所以考虑是不是应该利用不同的随机数(默认的随机数每次运行肯定是不变的)然后在某一特定的试验下进行多次求此系宗的平均值?)
( 3 ):对于复合增长率和实际收益,由于赌博次数很大,导致复合增长率差很小的情况下最终的收益会天壤之别。
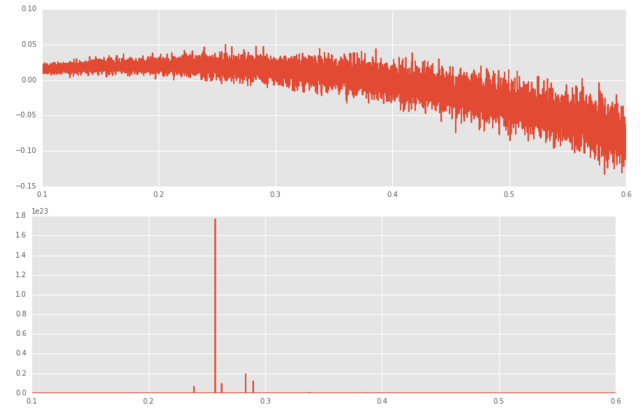
经多次模拟还是不能在 0.2 处取到最大值。请教 V2EX 大神们原因可能出在哪些方面?
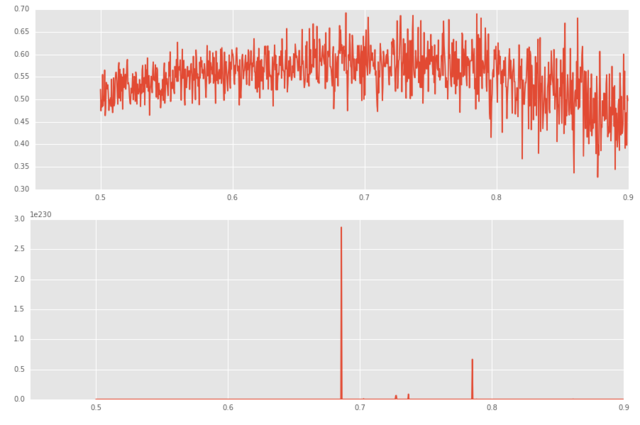
下面修改 p=0.8 a=2 b=-1 f_theroy=0.7
https://uqer.io/community/share/583baaf8228e5b49ef4ac73f
一:先介绍一下凯利公式: https://uqer.io/community/share/583baaf8228e5b49ef4ac73f
凯利公式的简化公式: f=p-q/b f :投注金额占总资金的比例 p :获胜的概率; q=1-p b :赔率 凯利公式出处原文对赔率的定义: b is the number of dollars returned for a one-dollar bet( including that one dollar). 既然是 bet ,那么 b 是指 bet 后如果赢了拿回的钱,如果输了为 0. 比如,投注 1 元掷骰子,赢了获得 10 元(“不?”包含投入的 1 元),输了为 0 ,则赔率为 10.(实际上就是 r_1=1 r_2=10 f=p/r_1-q/r_2 (这是标准公式)) (注:原文强调是包含投入的一元,但我感觉应该是不包含投入的一元,否则赔率应该为 9)
二:数学上的证明 可以参考这个博客: https://uqer.io/community/share/583baaf8228e5b49ef4ac73f 实际上就是 max(g) _
三:进行模拟实验: 取参数 p=0.6 r_1=1 r_2=1 计算得: f=0.2=0.6/1-0.4/1 初始资金 100 元 , 进行 1000 次赌博,令 f 分别为从 0.1-0.3 (分度值为 100 ) 进行试验。记录 f 值和对应的最后资金大小 和 复合收益率



实验分析:修改赌博次数 修改 div 分度值 存在的问题: https://uqer.io/community/share/583baaf8228e5b49ef4ac73f
( 1 ):按道理来讲应该是在 f=0.2 的时候 (确实是平稳随机过程)
( 2 ):混沌效应很明显 (原因可能是由于随机性在其中,对于 f 的微小改变在赌博多次后结果会差别巨大)(所以考虑是不是应该利用不同的随机数(默认的随机数每次运行肯定是不变的)然后在某一特定的试验下进行多次求此系宗的平均值?)
( 3 ):对于复合增长率和实际收益,由于赌博次数很大,导致复合增长率差很小的情况下最终的收益会天壤之别。

经多次模拟还是不能在 0.2 处取到最大值。请教 V2EX 大神们原因可能出在哪些方面?
下面修改 p=0.8 a=2 b=-1 f_theroy=0.7

https://uqer.io/community/share/583baaf8228e5b49ef4ac73f
1
bigtan 2016 年 11 月 29 日
凯利公式数学推导参考他的不如参考我的: https://estan.cn/2016/09/mathematical-derivation-of-kelly-formula.html
|