这是一个创建于 1604 天前的主题,其中的信息可能已经有所发展或是发生改变。
假设你是一个专业的窃贼,准备沿着一条街打劫房屋。每个房子都存放着特定金额的钱。你面临的唯一约束条件是:相邻的房子装着相互联系的防盗系统,且 当相邻的两个房子同一天被打劫时,该系统会自动报警。 给定一个非负整数列表,表示每个房子中存放的钱, 算一算,如果今晚去打劫,在不触动报警装置的情况下, 你最多可以得到多少钱 。
在线评测地址: https://www.lintcode.com/problem/house-robber/?utm_source=sc-v2ex-fks
样例 1:
输入: [3, 8, 4]
输出: 8
解释: 仅仅打劫第二个房子.
样例 2:
输入: [5, 2, 1, 3]
输出: 8
解释: 抢第一个和最后一个房子
[题解]
解题思路:
由抢房屋的性质可以看出,抢前 i 个房屋能得到的最大值,与后面如何抢的方案无关,只与前 i - 1 个房屋的最优方案有关。这满足了动态规划的无后效性和最优子结构。同时,由于题目不能抢相邻房屋,那么如果抢了第 i 个房屋,就不能抢第 i - 1 个房屋,可以得出前 i 个的最优方案也与前 i - 2 个的最优方案有关。
代码思路:
可以设 dp(i, 0)为如果不抢第 i 个房屋,前 i 个房屋的最优方案为多少;设 dp(i, 1)为如果抢第 i 个房屋,前 i 个房屋的最优方案为多少。可以得出以下的状态转移方程式:
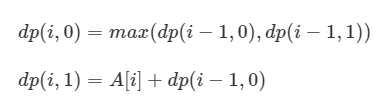 复杂度分析
复杂度分析
设房屋数量为 N 。 时间复杂度
- 扫描一遍数组,每次 O(1)时间动态转移,复杂度为 O(N)。 空间复杂度
- dp 数组的规模为 N * 2,空间复杂度为 O(N)。
- 在空间上可以有一个小优化,对于计算第 i 个房屋时,有关的数据只有(i - 1) ~ i 三组数据,可以每次只记录这两组数据,并在转移后丢弃掉最早的,加上新的数据,进入下一个循环继续计算。空间复杂度为 O(1)。
public class Solution {
/**
* @param A: An array of non-negative integers
* @return: The maximum amount of money you can rob tonight
*/
public long houseRobber(int[] A) {
int n = A.length;
if (n == 0) {
return 0;
}
long[][] dp = new long[n][2];
dp[0][0] = 0;
dp[0][1] = A[0];
for (int i = 1; i < n; i++) {
// 如果不抢第 i 个,取前 i - 1 个位置 dp 较大值
dp[i][0] = Math.max(dp[i - 1][0], dp[i - 1][1]);
// 如果抢第 i 个,前一个不抢,考虑从前 i - 2 个位置的 dp 值转移
dp[i][1] = A[i] + dp[i - 1][0];
}
long result = Math.max(dp[n - 1][0], dp[n - 1][1]);
return result;
}
}
更多题解参见:https://www.jiuzhang.com/solution/house-robber/?utm_source=sc-v2ex-fks
目前尚无回复