推荐学习书目
› Learn Python the Hard Way
Python Sites
› PyPI - Python Package Index
› http://diveintopython.org/toc/index.html
› Pocoo
值得关注的项目
› PyPy
› Celery
› Jinja2
› Read the Docs
› gevent
› pyenv
› virtualenv
› Stackless Python
› Beautiful Soup
› 结巴中文分词
› Green Unicorn
› Sentry
› Shovel
› Pyflakes
› pytest
Python 编程
› pep8 Checker
Styles
› PEP 8
› Google Python Style Guide
› Code Style from The Hitchhiker's Guide
这是一个创建于 1923 天前的主题，其中的信息可能已经有所发展或是发生改变。
现在已知 4 个坐标经纬度围成了一个矩形，如何在这个已知矩形中生成 500 个等距的经纬度坐标点呢？
第 1 条附言 · 2019-08-21 09:56:27 +08:00
sorry 各位,可能描述的不太清楚
是这样 我这有一个上海市经纬度的小区分布数据,我用 dbscan 聚类了一下,但是不管怎么调整参数,在中心最密集的几个区都会出现空洞,猜测应该是样板分布不均的原因,所以我想在这个区域看用什么方法能生成一个平均分布的点
是这样 我这有一个上海市经纬度的小区分布数据,我用 dbscan 聚类了一下,但是不管怎么调整参数,在中心最密集的几个区都会出现空洞,猜测应该是样板分布不均的原因,所以我想在这个区域看用什么方法能生成一个平均分布的点
 |
1
xuanbg 2019-08-20 17:46:57 +08:00
除非矩形的长宽比是固定的几个值，否则不可能存在解
|
 |
2
no1xsyzy 2019-08-20 18:21:52 +08:00
等距是怎么个定义法？是矩形排列还是六边形排列？平面距离还是空间距离？是必须包含边界还是不需要？
你什么都不说别人怎么回答？楼上楼下除了给出 8 个答案的其他都是在瞎猜。 |
 |
3
bilibilifi 2019-08-20 18:24:30 +08:00 via iPhone
经纬度的话涉及到不同国家和地区的参考系，是一个很麻烦的问题
|
 |
4
SeanChense 2019-08-20 18:27:36 +08:00 via iPhone
两个点是线段，三个点是等边三角形，四个点是啥
|
|
5
bilibilifi 2019-08-20 18:31:42 +08:00 via iPhone
同一个参考系的话可以利用库就 ok，不同的话要计算投影
|
 |
6
necomancer 2019-08-20 19:40:37 +08:00
不知道你说的等距是啥概念，如果想求的是均分球面，等价于求 \theta\in(0, \theta), \phi\in(0, \phi) 的 500 个单位向量中，\sum_ij 1/|r_i - r_j| 的最小值，是一个有区域限制的汤普森问题。
初始化生成 500 个单位向量，在 0<theta<经度, 0<phi<维度 满足你的矩形限制条件下，最小化能量函数 U(r1,r2,...r500)=\sum_{i=1}^500 1/|r_i-r_j|，mathematica 有比较简单的代码。要自己撸需要用梯度下降法，或者参考 scipy.optimize 里的 minimize 函数。 |
|
7
necomancer 2019-08-20 19:42:31 +08:00
如果是均分经度、维度，那么 1 楼说了，需要特定的长宽比。上面均分球面算法保证弧线、弦距离相等。
|
|
8
necomancer 2019-08-20 19:55:03 +08:00
如果你不需要那么精确的结果，也可以考虑直接用密度，也就是如果你的矩形所占球台面积是 10，那么密度就是 50，如果球面积是 200，那么总点数就是 200x50=10000，Mathematica 有个 SpherePoints 函数，可以生成很均匀的点，大量点精确度会变高而且速度很快，详见 Fejes Tóth 问题。速度很快。你可以生成好以后用矩形去框一下，密度法可能有一定的涨落，如果要求结果不用那么精确的话（ 500+-10 ），这个方法是最高效的。
|
 |
9
opengps 2019-08-20 20:44:34 +08:00
这种需求是网格处理方面的算法吗？
|
 |
10
chengxiao OP |
|
11
necomancer 2019-08-21 10:22:23 +08:00
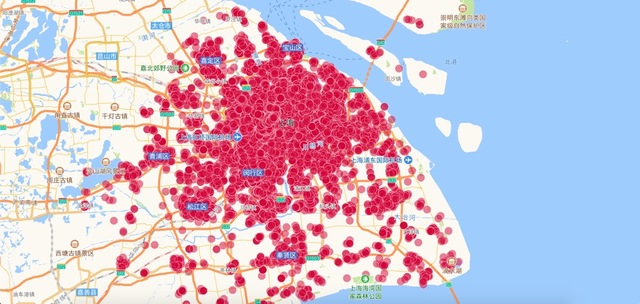
球面均匀点的算法我在之前已经提供了，看起来你并不是绝对需要 500 个点，你可以考虑尝试 Mathematica 的 SpherePoints 函数，等距性很好。我没能理解你的 dbscan 是怎么做的，空洞是什么意思？从图 1 来看感觉所有点都是连在一起的。你是直接对 (经，纬，1 ）这样相当于对经纬度分类还是每个小区有不同的权重？ dbscan 基于密度，加上权重也许你的问题就能解决了。另外，你可以试试 hdbscan 算法。
|
|
12
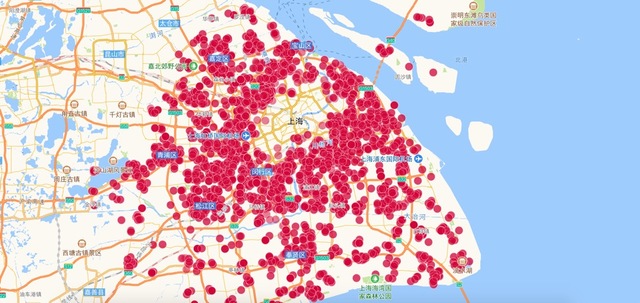
chengxiao OP @necomancer 权重是一样的 直接队经纬度进行聚类 图二上能看到上海最密的区域是个空洞 没有 1 个点，但从图 1 可以看出那里是最密集的区域
|
|
14
chengxiao OP @necomancer 感谢 信息量有点大 我先消化消化....激动到发错了
|
 |
15
Raymon111111 2019-08-21 10:53:51 +08:00
geohash 块的中心就行
|
Select Language