这是一个创建于 3370 天前的主题,其中的信息可能已经有所发展或是发生改变。
小伙伴们,感谢大家一个周末的等待『认真脸』~在上篇中,我们向大家简单介绍了 Logistic Regression 的数学模型,尝试推导并详细解释了求解最优回归系数的过程。今天,我们将向大家分享 Python 实现 Logistic Regression 的基本版,介绍 sklearn 中的 Logistic Regression 算法及其关键参数以及如何实现一个基于 Logistic Regression 的简单选股策略。准备好了吗?系好安全带,让我们开始吧!

PS :为了保证部分代码的展示质量,查看详细代码请移步传送门: https://uqer.io/community/share/5788af62228e5b8a03932cc5 ,小伙伴们也可以从中查看完整帖子,蟹蟹~
1 、 Python 实现 Logistic Regression 的基本版

1.1 准备数据:
从网上整理了一组数据: 前两列元素是 feature ;最后一列是 label ,其值是 0 或 1 。
传送门: https://uqer.io/community/share/5788af62228e5b8a03932cc5
1.2 数据预处理
包括:

1.3 定义 Logistic 函数:
def logit(z):
'''
logistic function 即:
牛顿迭代公式中的 p(yi=1 | xi; w)
'''
return 1.0 / (1.0 + np.exp(-z))
1.4 梯度上升法算法:
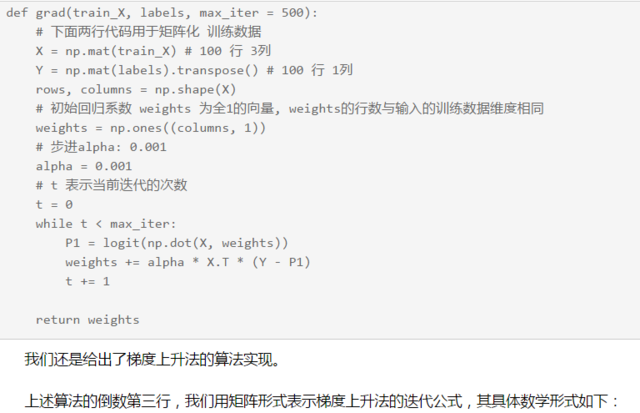
$$
\left[
\begin{matrix}
\omega_0 \
\omega_1 \
\omega_2
\end{matrix}
\right]^{(t+1)}
=
\left[
\begin{matrix}
\omega_0 \
\omega_1 \
\omega_2
\end{matrix}
\right]^{(t)}
\alpha \left[ \begin{matrix} 1.0 & x{11} & x{12} \ 1.0 & x{21} & x{22} \ \vdots & \vdots & \vdots \ 1.0 & x{n1} & x{n2} \ \end{matrix} \right]^{\text{T}}
\left[
\left(
y1 y2 ⋮ yn
\right)
-
\left(
p1(x1;ω) p1(x2;ω) ⋮ p1(xn;ω)
\right)
\right]
$$
1.5 牛顿法算法:

在本节的牛顿算法中, Hessian 矩阵具体数学形式如下:
$$
Hessian =
\left[
\begin{matrix}
1.0 & x{11} & x{12} \
1.0 & x{21} & x{22} \
\vdots & \vdots & \vdots \
1.0 & x{n1} & x{n2} \
\end{matrix}
\right]^{\text{T}}
\left[p1(x1;ω)(p1(x1;ω)−1) p1(x2;ω)(p1(x2;ω)−1) ⋱ p1(xn;ω)(p1(xn;ω)−1)
\right]
\left[
\begin{matrix}
1.0 & x{11} & x{12} \
1.0 & x{21} & x{22} \
\vdots & \vdots & \vdots \
1.0 & x{n1} & x{n2} \
\end{matrix}
\right]
$$
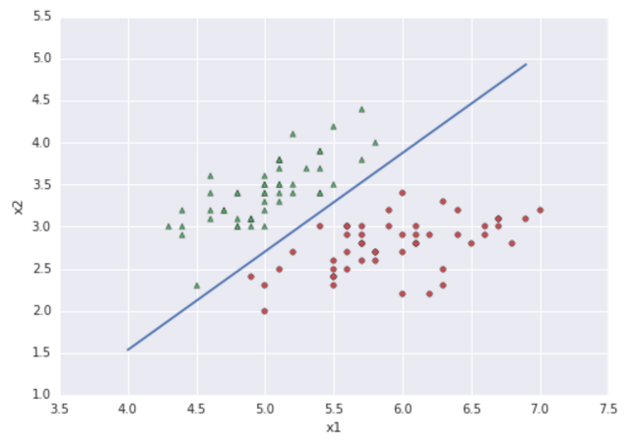
1.6 选择最优算法,根据求得的最优系数画出回归直线:
传送门: https://uqer.io/community/share/5788af62228e5b8a03932cc5
1.7 下面一个 cell 运行整段代码:
传送门: https://uqer.io/community/share/5788af62228e5b8a03932cc5
2 、 sklearn 中的 Logistic Regression 算法:
sklearn 是 Python 实现的开源机器学习算法包,优矿正好也支持它。下面简单介绍下 sklearn 中 Logistic Regression 的使用。
2.1 实例化 Logistic Regression :

在本问题中,我们将极大似然函数的负值视为代价函数,代价函数越小,说明极大似然函数越大,说明模型分类的准确性越高;
CωTω 用以衡量模型复杂度, C 用以控制原代价函数与模型复杂度之间的折中。
很显然, C 越大,算法对模型复杂度越敏感。
2.2 训练数据:
lr.fit(train_X, labels)
其中, train_X 表示的训练数据的特征,其格式 n 行 m 列的矩阵, n 为训练数据的个数, m 为数据的特征个数(维度);
labels 表示的训练数据的类别,格式为 n 行 1 列的列向量。
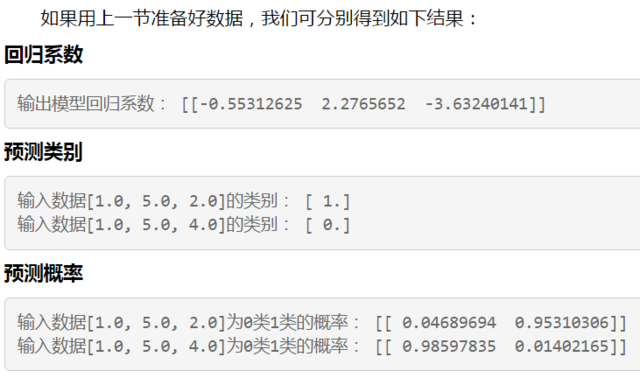
2.3 输出模型系数,输出测试数据的类别与概率:
# 回归系数
print '输出模型回归系数:', lr.coef_
print '\n'
# 预测类别
print '输入数据[1.0, 5.0, 2.0]的类别:', lr.predict([1.0, 5.0, 2.0])
print '输入数据[1.0, 5.0, 4.0]的类别:', lr.predict([1.0, 5.0, 4.0])
print '\n'
# 预测概率
print '输入数据[1.0, 5.0, 2.0]为 0 类 1 类的概率:', lr.predict_proba([1.0, 5.0, 2.0])
print '输入数据[1.0, 5.0, 4.0]为 0 类 1 类的概率:', lr.predict_proba([1.0, 5.0, 4.0])
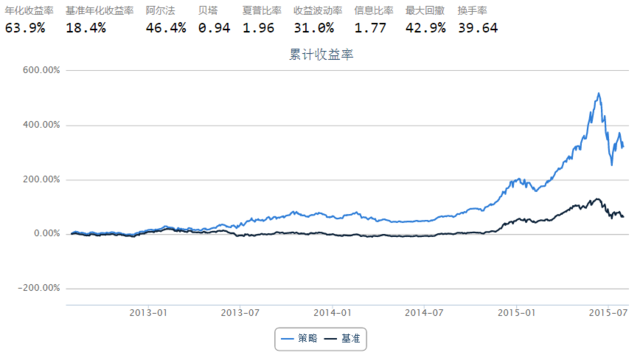
3. 基于 Logistic Regression 的简单选股策略:

下面的 cell 给出策略代码及回测结果:
各位大大有什么看法,欢迎讨论哦~

PS :为了保证部分代码的展示质量,查看详细代码请移步传送门: https://uqer.io/community/share/5788af62228e5b8a03932cc5 ,小伙伴们也可以从中查看完整帖子,蟹蟹~
1 、 Python 实现 Logistic Regression 的基本版

1.1 准备数据:
从网上整理了一组数据: 前两列元素是 feature ;最后一列是 label ,其值是 0 或 1 。
传送门: https://uqer.io/community/share/5788af62228e5b8a03932cc5
1.2 数据预处理
包括:

1.3 定义 Logistic 函数:
def logit(z):
'''
logistic function 即:
牛顿迭代公式中的 p(yi=1 | xi; w)
'''
return 1.0 / (1.0 + np.exp(-z))
1.4 梯度上升法算法:

$$
\left[
\begin{matrix}
\omega_0 \
\omega_1 \
\omega_2
\end{matrix}
\right]^{(t+1)}
=
\left[
\begin{matrix}
\omega_0 \
\omega_1 \
\omega_2
\end{matrix}
\right]^{(t)}
\alpha \left[ \begin{matrix} 1.0 & x{11} & x{12} \ 1.0 & x{21} & x{22} \ \vdots & \vdots & \vdots \ 1.0 & x{n1} & x{n2} \ \end{matrix} \right]^{\text{T}}
\left[
\left(
y1 y2 ⋮ yn
\right)
-
\left(
p1(x1;ω) p1(x2;ω) ⋮ p1(xn;ω)
\right)
\right]
$$
1.5 牛顿法算法:

在本节的牛顿算法中, Hessian 矩阵具体数学形式如下:
$$
Hessian =
\left[
\begin{matrix}
1.0 & x{11} & x{12} \
1.0 & x{21} & x{22} \
\vdots & \vdots & \vdots \
1.0 & x{n1} & x{n2} \
\end{matrix}
\right]^{\text{T}}
\left[p1(x1;ω)(p1(x1;ω)−1) p1(x2;ω)(p1(x2;ω)−1) ⋱ p1(xn;ω)(p1(xn;ω)−1)
\right]
\left[
\begin{matrix}
1.0 & x{11} & x{12} \
1.0 & x{21} & x{22} \
\vdots & \vdots & \vdots \
1.0 & x{n1} & x{n2} \
\end{matrix}
\right]
$$
1.6 选择最优算法,根据求得的最优系数画出回归直线:
传送门: https://uqer.io/community/share/5788af62228e5b8a03932cc5
1.7 下面一个 cell 运行整段代码:
传送门: https://uqer.io/community/share/5788af62228e5b8a03932cc5

2 、 sklearn 中的 Logistic Regression 算法:
sklearn 是 Python 实现的开源机器学习算法包,优矿正好也支持它。下面简单介绍下 sklearn 中 Logistic Regression 的使用。
2.1 实例化 Logistic Regression :

在本问题中,我们将极大似然函数的负值视为代价函数,代价函数越小,说明极大似然函数越大,说明模型分类的准确性越高;
CωTω 用以衡量模型复杂度, C 用以控制原代价函数与模型复杂度之间的折中。
很显然, C 越大,算法对模型复杂度越敏感。
2.2 训练数据:
lr.fit(train_X, labels)
其中, train_X 表示的训练数据的特征,其格式 n 行 m 列的矩阵, n 为训练数据的个数, m 为数据的特征个数(维度);
labels 表示的训练数据的类别,格式为 n 行 1 列的列向量。
2.3 输出模型系数,输出测试数据的类别与概率:
# 回归系数
print '输出模型回归系数:', lr.coef_
print '\n'
# 预测类别
print '输入数据[1.0, 5.0, 2.0]的类别:', lr.predict([1.0, 5.0, 2.0])
print '输入数据[1.0, 5.0, 4.0]的类别:', lr.predict([1.0, 5.0, 4.0])
print '\n'
# 预测概率
print '输入数据[1.0, 5.0, 2.0]为 0 类 1 类的概率:', lr.predict_proba([1.0, 5.0, 2.0])
print '输入数据[1.0, 5.0, 4.0]为 0 类 1 类的概率:', lr.predict_proba([1.0, 5.0, 4.0])

3. 基于 Logistic Regression 的简单选股策略:

下面的 cell 给出策略代码及回测结果:

各位大大有什么看法,欢迎讨论哦~
4 条回复 • 2016-12-13 16:49:11 +08:00
1
lixuda 2016 年 12 月 13 日
看你收益率都是牛市的时候,那个时候随便一只股票,特别小盘股,都轻轻松松跑赢大盘。你看看熊市的时候。
|
2
aries1998 2016 年 12 月 13 日
永远别信 backtest, 你如果根据 backtest 来调整参数和策略, 只不过是在骗自己而已
|
3
aries1998 2016 年 12 月 13 日
或者说得更直白一点, 你得先有一套自己成功操作策略, 长期验证成功的, 然后再用代码来落地这套策略, 而不是"想"出一个策略来指望赚钱. 最简单的, 你这种日线级别的, 怎么判定盘整 /趋势都没法解决, 这个我觉得是解决不了的事情, 预测更是别想了, 当你想预测的时候, 你就离死不远了. 更多应该考虑的是行情的量化分类, 以及不同分类下怎么处理.
|