这是一个创建于 3325 天前的主题,其中的信息可能已经有所发展或是发生改变。
前言
梯度下降法( Gradient Descent )是机器学习中最常用的优化方法之一,常用来求解目标函数的极值。
其基本原理非常简单:沿着目标函数梯度下降的方向搜索极小值(也可以沿着梯度上升的方向搜索极大值)。
在《 [ Python 机器学习] 梯度下降法(一)》中简单分析了学习率大小对搜索过程的影响,发现:
学习率较小时,收敛到极值的速度较慢。
学习率较大时,容易在搜索过程中发生震荡。
在《 [ Python 机器学习] 梯度下降法(二)》中简单分析了冲量对搜索过程的影响,发现:
在学习率较小的时候,适当的 momentum 能够起到一个加速收敛速度的作用。
在学习率较大的时候,适当的 momentum 能够起到一个减小收敛时震荡幅度的作用。
接下来介绍梯度下降法中的第三个超参数: decay 。
学习率衰减因子: decay
为了板式的清晰,完整回测代码请戳: https://uqer.io/community/share/5820515e228e5ba8f5571953
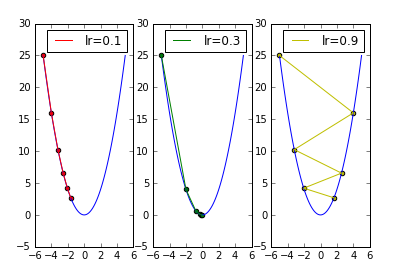
从上图可看出,学习率较大时,容易在搜索过程中发生震荡,而发生震荡的根本原因无非就是搜索的步长迈的太大了。
在使用梯度下降法求解目标函数 func(x) = x * x 的极小值时,更新公式为 x += v ,其中每次 x 的更新量 v 为 v = - dx * lr , dx 为目标函数 func(x) 对 x 的一阶导数。如果能够让 lr 随着迭代周期不断衰减变小,那么搜索时迈的步长就能不断减少以减缓震荡。学习率衰减因子由此诞生:
lr_i = lr_start * 1.0 / (1.0 + decay * i)
上面的公式即为学习率衰减公式,其中 lr_i 为第 i 次迭代时的学习率, lr_start 为原始学习率, decay 为 一个介于[0.0, 1.0]的小数。
decay 越小,学习率衰减地越慢,当 decay = 0 时,学习率保持不变。
decay 越大,学习率衰减地越快,当 decay = 1 时,学习率衰减最快。
测试以及绘图代码如下: https://uqer.io/community/share/5820515e228e5ba8f5571953
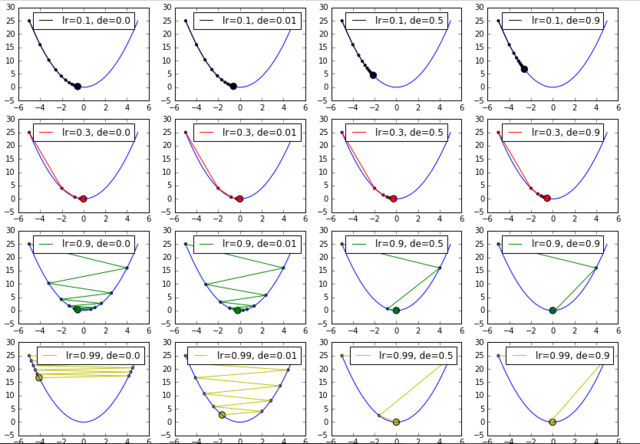
在所有行中均可以看出, decay 越大,学习率衰减地越快。
在第三行与第四行可看到, decay 确实能够对震荡起到减缓的作用。
起始学习率为 1.0
decay 为[0.0, 0.001, 0.1, 0.5, 0.9, 0.99]
迭代周期为 300
测试以及绘图代码如下: https://uqer.io/community/share/5820515e228e5ba8f5571953
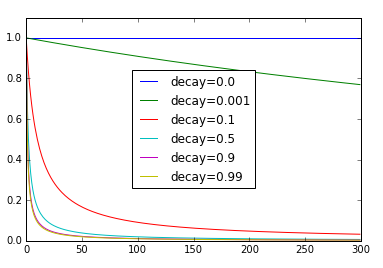
可以看到,当 decay 为 0.1 时, 50 次迭代后学习率已从 1.0 急剧降低到了 0.2 。如果 decay 设置得太大,则可能会收敛到一个不是极值的地方呢。
梯度下降法( Gradient Descent )是机器学习中最常用的优化方法之一,常用来求解目标函数的极值。
其基本原理非常简单:沿着目标函数梯度下降的方向搜索极小值(也可以沿着梯度上升的方向搜索极大值)。
在《 [ Python 机器学习] 梯度下降法(一)》中简单分析了学习率大小对搜索过程的影响,发现:
学习率较小时,收敛到极值的速度较慢。
学习率较大时,容易在搜索过程中发生震荡。
在《 [ Python 机器学习] 梯度下降法(二)》中简单分析了冲量对搜索过程的影响,发现:
在学习率较小的时候,适当的 momentum 能够起到一个加速收敛速度的作用。
在学习率较大的时候,适当的 momentum 能够起到一个减小收敛时震荡幅度的作用。
接下来介绍梯度下降法中的第三个超参数: decay 。
学习率衰减因子: decay
为了板式的清晰,完整回测代码请戳: https://uqer.io/community/share/5820515e228e5ba8f5571953

从上图可看出,学习率较大时,容易在搜索过程中发生震荡,而发生震荡的根本原因无非就是搜索的步长迈的太大了。
在使用梯度下降法求解目标函数 func(x) = x * x 的极小值时,更新公式为 x += v ,其中每次 x 的更新量 v 为 v = - dx * lr , dx 为目标函数 func(x) 对 x 的一阶导数。如果能够让 lr 随着迭代周期不断衰减变小,那么搜索时迈的步长就能不断减少以减缓震荡。学习率衰减因子由此诞生:
lr_i = lr_start * 1.0 / (1.0 + decay * i)
上面的公式即为学习率衰减公式,其中 lr_i 为第 i 次迭代时的学习率, lr_start 为原始学习率, decay 为 一个介于[0.0, 1.0]的小数。
decay 越小,学习率衰减地越慢,当 decay = 0 时,学习率保持不变。
decay 越大,学习率衰减地越快,当 decay = 1 时,学习率衰减最快。
测试以及绘图代码如下: https://uqer.io/community/share/5820515e228e5ba8f5571953

在所有行中均可以看出, decay 越大,学习率衰减地越快。
在第三行与第四行可看到, decay 确实能够对震荡起到减缓的作用。
起始学习率为 1.0
decay 为[0.0, 0.001, 0.1, 0.5, 0.9, 0.99]
迭代周期为 300
测试以及绘图代码如下: https://uqer.io/community/share/5820515e228e5ba8f5571953

可以看到,当 decay 为 0.1 时, 50 次迭代后学习率已从 1.0 急剧降低到了 0.2 。如果 decay 设置得太大,则可能会收敛到一个不是极值的地方呢。
1
xiamx 2016 年 12 月 8 日
很棒! OP 什么时候讲一下 epoch 的作用和调参呢?
|